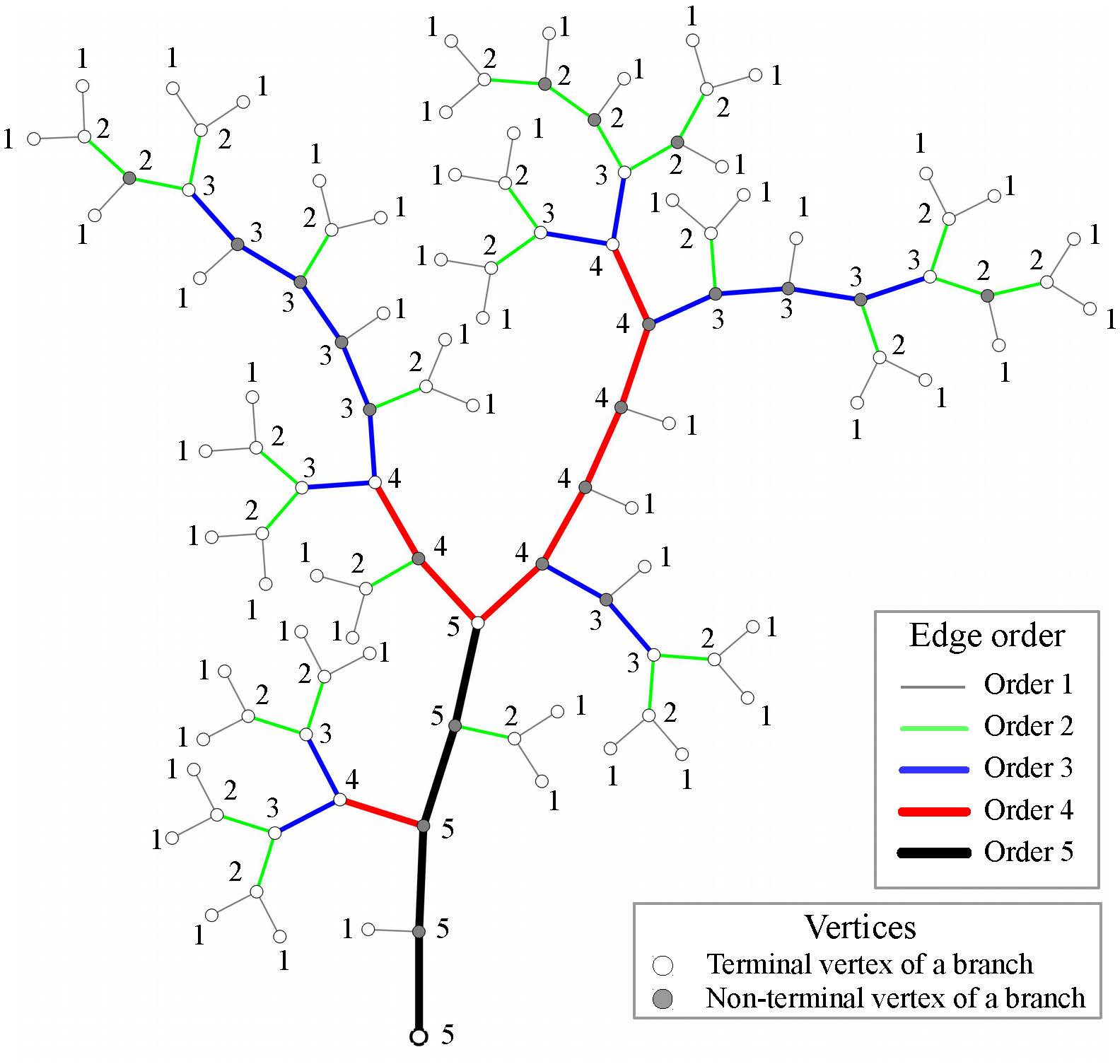
Horton-Strahler orders of vertices in a binary tree: example. The orders quantify importance of the elements in a hierarchy. Horton-Strahler orders and related Horton pruning are the key elements of the self-similar tree theory.
My research interests are in applied probability and statistic, with focus on
random self-similar trees and networks,
coalescent and branching processes,
random sums of heavy-tailed variables, and
time series analysis.
Applications include statistical seismology, structure of river channel networks,
and cell biology.
I'm looking for graduate and undergraduate research assistants -- please contact me at zal@unr.edu if you are intersted.
Available projects involve a combination of methodology development, data analysis, and/or numerical modeling.
Tree graphs (trees) are commonly used to describe river networks, neuronal forests of the nervous system, vascular networks, vein systems of leaves, and many other natural systems.
Trees are also important in representing time-dependent processes such as ancestral relations of species (phylogenetic trees), spread of a disease, or growth of fractures in solids.
It has been well documented since the 1980s that many observed tree hierarchies are self-similar – they do not change they basic statistical properties after changing the scale of examination (zooming in or out).
The theory of random self-similar trees offers a rigorous modeling framework that is
mathematically tractable and flexible enough to closely fit diverse observations.

Horton-Strahler orders of vertices in a binary tree: example.
The orders quantify importance of the elements in a hierarchy.
Horton-Strahler orders and related Horton pruning are the key elements of the self-similar tree theory.
How large earthquakes are generated and how their preparation processes might be tracked with observable signals
remain fundamental unsolved scientific questions, with substantial societal and economic importance.
Large earthquakes can produce devastating destruction and loss of life directly, and trigger additional
hazards such as fires and landslides.
My research focuses on statistical analysis of earthquake clustering (including the problem of catalog declustering)
and localization of seismicity prior to large earthquakes.
It is a part of a broader community effort to combine novel statistical techniques, high-quality earthquake catalogs,
data from laboratory fracturing experiments and physical modeling to improve the ability to understand the preparation
process of large failure events.
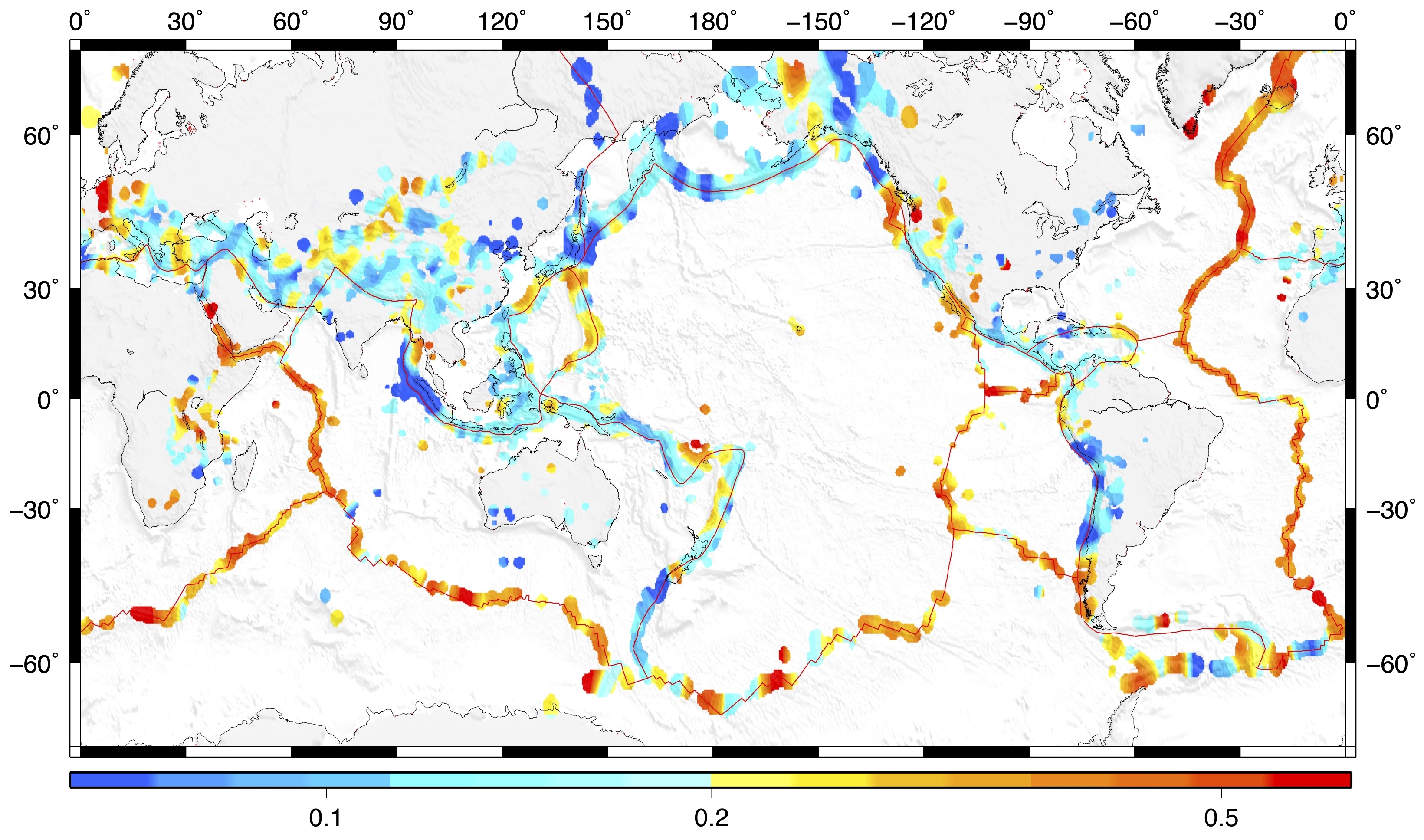
Proportion of foreshocks in the eqrthquake clusters around the world (M>4).
It is evident that the structure of earthquake clusters changes from place to place.
Identifying earthquake clusters and relating their structure to the physical properties
of the lithosphere, as well as to the timing within the earthquake cycle, are among the
problems of statistical seismology.
The hierarchical organization and self-similarity in river basins have been topics of extensive re-
search in hydrology and geomorphology starting with the pioneering work of Horton in 1945.
My research is focused on developing mathematical models that clarify the origin of Horton laws,
Hack's laws, basin fractal dimension, power-law distributions of link attributes, and power-law relations
between distinct attributes.
The main technical tool is the theory of random self-similar trees.
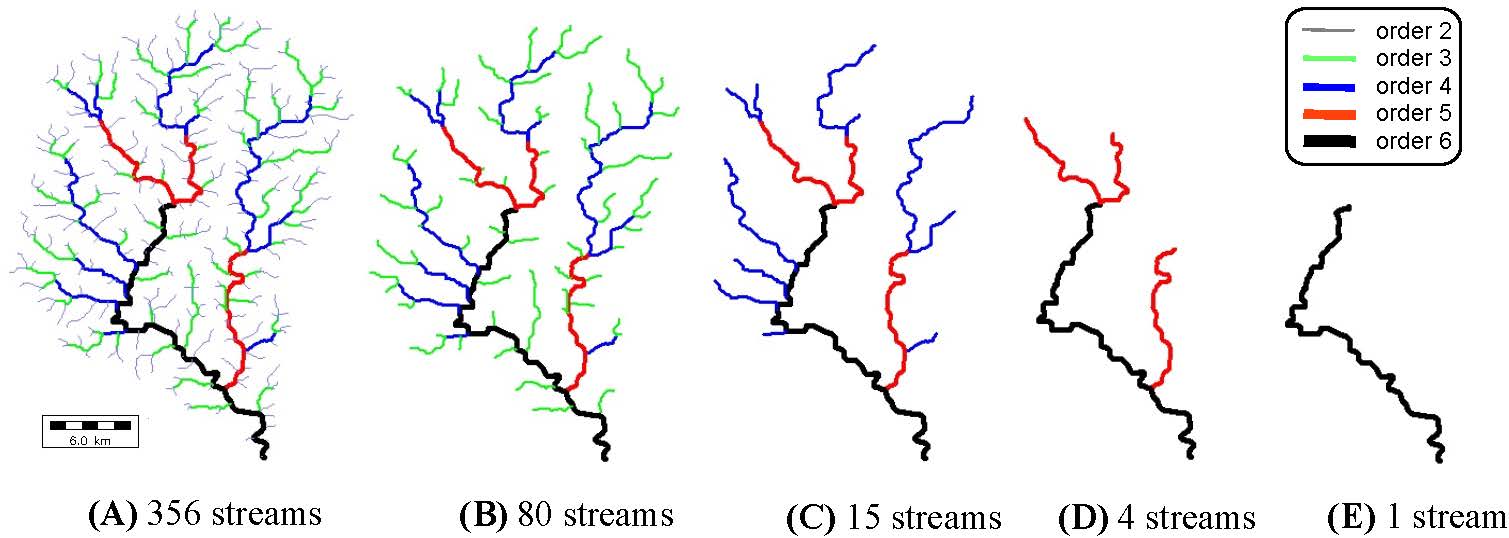
Stream network of Beaver creek, Floyd County, KY.
Colors show streams of different Horton-Strahler orders.
Different panels refer to consecutive Horton prunings of the network -- cutting the outmost streams (or,
streams of the lowest order).
Horton-Strahler orders and Horton pruning are the key elements of the self-similar tree theory that
explains multiple scalings in the river networks.